The Veil of Precision: Uncertainty Principle
By : Ali Hamza
In our everyday lives, we often measure and understand the world around us. Whether it's recording a racer’s speed with a stopwatch or using a GPS to mark a location, our tools and methods give us a clear and accurate answer in the macroscopic world. However, when we shift our focus to the unseen world of particles like electrons and photons, these straightforward measurements become a bit limited by the principles of quantum mechanics.
Understanding Heisenberg's Uncertainty Principle
Discovered and observed by the German physicist Heisenberg in 1927, the uncertainty principle is an important concept in quantum mechanics. It states that we cannot know both the position and speed of a particle, such as a photon or electron, with perfect accuracy; the more we accurately scale down the particle's position, the less we know about its speed, and vice versa.
Everyday vs. Quantum Measurements
In everyday life, calculating the speed and position of a moving object is relatively straightforward. For instance, we can measure a car travelling at 60 miles per hour or a tortoise crawling at 0.5 miles per hour and simultaneously pinpoint where the objects are located. However, in the quantum world of particles, making these calculations is not possible due to the uncertainty principle [1].
The Uncertainty Principle Explained
Heisenberg’s uncertainty principle states that it is impossible to measure or calculate exactly both the position and the momentum of an object. This principle is based on the wave-particle duality of matter. Although Heisenberg’s uncertainty principle can be ignored in the macroscopic world (where the uncertainties in the position and velocity of objects with relatively large masses are negligible), it holds significant value in the quantum world [2]. Since atomic particles have very small masses, any increase in the accuracy of their positions will cause an increase in the uncertainty associated with their velocities.
Why Is It Impossible to Measure Both Position and Momentum Simultaneously?
In order to measure the position of an object, a photon must collide with it and return to the measuring device. Since photons hold some momentum, a transfer of momentum will occur when the photon collides with the electron. This transfer of momentum will cause the momentum of the electron to increase. Thus, any attempt at measuring the position of a particle will increase the uncertainty in the value of its momentum.
Applying the same example to a macroscopic object (say a basketball), it can be understood that Heisenberg’s uncertainty principle has a negligible impact on measurements in the macroscopic world. While measuring the position of a basketball, there will still be a transfer of momentum from the photons to the ball. However, the mass of the photon is much smaller than the mass of the ball. Therefore, any momentum transferred by the photon to the ball can be neglected [3].
Mathematical Representation
The uncertainty principle can be mathematically represented as follows:
ħ = value of Planck’s constant divided by 2π
∆X = uncertainty in the position
∆p = uncertainty in momentum
∆E = uncertainty in the energy
∆t = uncertainty in time measurement
The principle asserts that the product of the uncertainty in position (∆X) and the uncertainty in momentum (∆p) of a particle cannot be smaller than a certain value, specifically (ħ/2). This means that the more precisely we know the position of a particle, the less precisely we can know its momentum, and vice versa. [4]
Conclusion
Heisenberg’s uncertainty principle is a pillar of quantum mechanics, highlighting the limitations and problems in our ability to measure the properties of particles. While its effects are negligible in the macroscopic world, they are significant in the quantum world.
References
2. https://byjus.com/jee/heisenberg-uncertainty-principle/


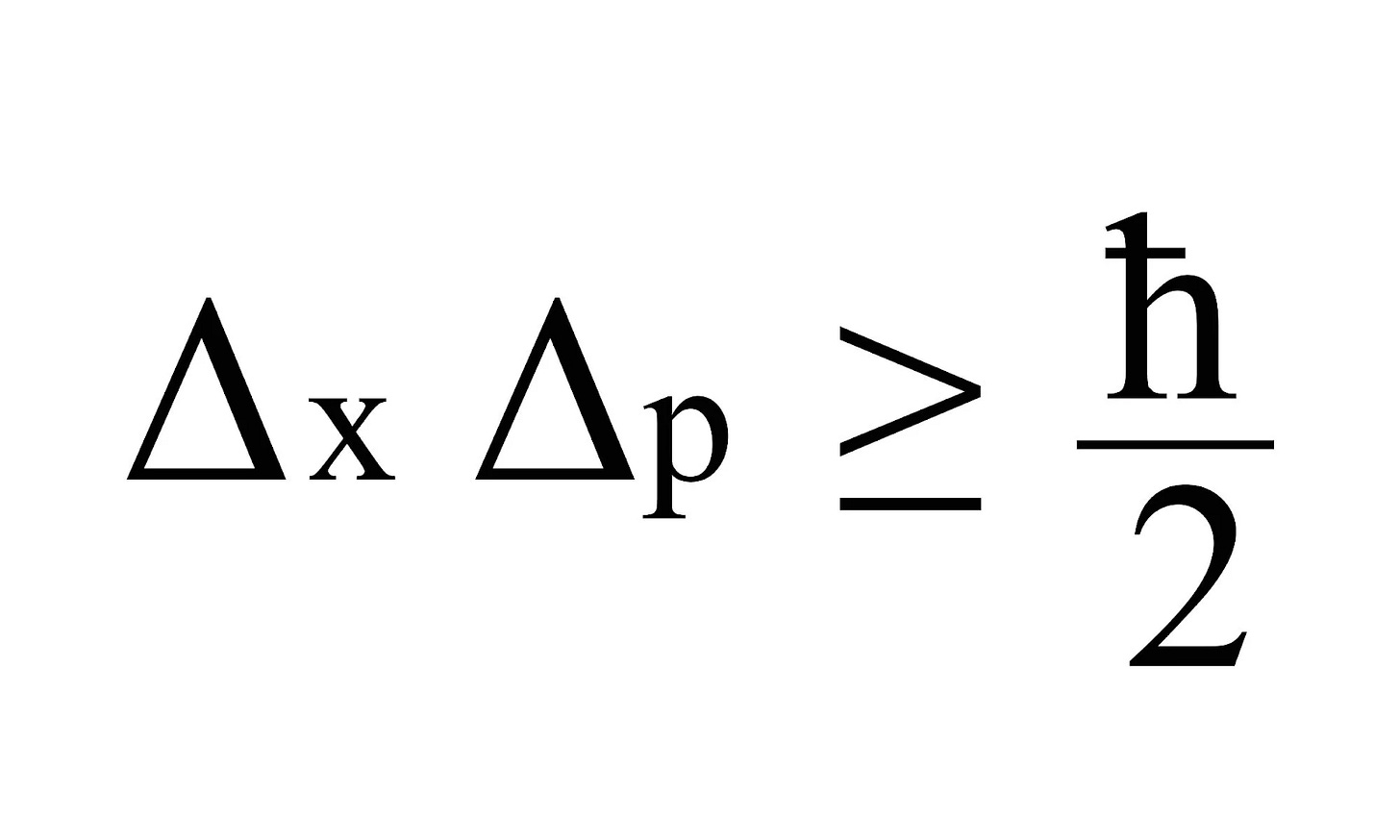
eyes do lie , Chico ;)